This is an example of nonuniform circular motion.
The component of the particle's acceleration in the tangential direction is given by 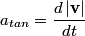 where 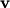 is the particle's velocity. The component of the particle's acceleration in the radial direction is is the particle's velocity. The component of the particle's acceleration in the radial direction is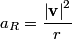 We are given that 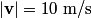 and and 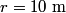 . Therefore, . Therefore,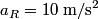 We are also given that 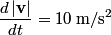 , therefore, , therefore,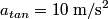 So, the tangential and the radial component of the particle's acceleration have the same magnitude. Therefore, the resultant acceleration vector makes a 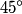 angle with each of them. The particle's velocity vector also points in the tangential direction, therefore, the resultant acceleration vector makes a angle with each of them. The particle's velocity vector also points in the tangential direction, therefore, the resultant acceleration vector makes a 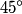 angle with it also. Therefore, answer (C) is correct. angle with it also. Therefore, answer (C) is correct. |